Samuel Tenka

Eraser

Arghh! Whenever I photograph a drawing, it turns out all dark --- and not even uniformly so!

copy of WIND by the great print-maker Hokusai

So I wrote a program to guess how much is paper:

estimated lighting artifacts

and how much is drawing:

cleaned drawing

Wow! I'm surprised it worked! I barely had to change my initial guess at an algorithm; mainly, I just converted previously integer arithmetic to floating point so I could mess around with tiny timesteps . . . speaking of which, yeah, how does it work?

This way: to find out how the image looks like erased, we physically simulate a sheet of cloth, which "falls down" on the graph of the image, where white is high and black, low. Tension in the fabric will prevent it from filling black valleys, so we'll get some surface that fits neatly on the highest parts of the image, but that remains far above low parts. In other words, we will have whitened out the black areas in a smooth way consistent with the bad lighting of the white areas. The fabric is then a graph of the paper beneath the drawing!

decomposition of a 1D image into foreground and background

convergence of iterative approximations

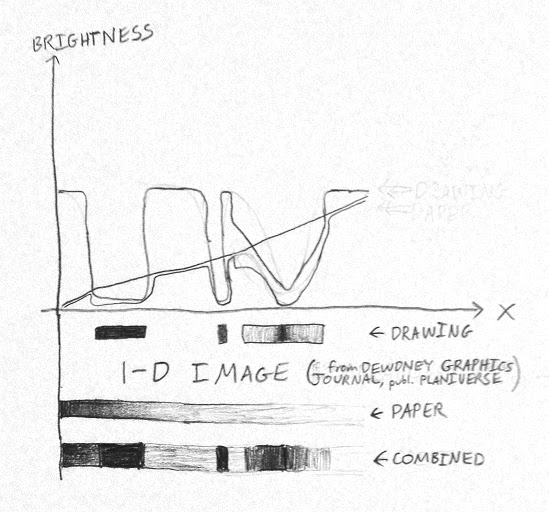
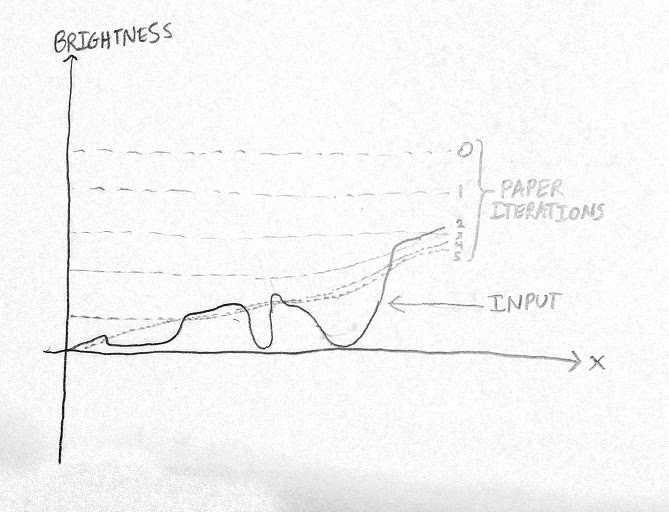
In particular, we want to minimize the energy $V:\text{bitmaps} \to \mathbb{R}$: $$\text{to do} = \text{fall down} + \text{catch on original} + \text{don't warp}$$ $$V(p) = m p + k \min\{0, \, (p-\text{original})\}^2 + s (\nabla^2 p)^2$$ and so descend by gradient $$\text{paper} \leftarrow \text{paper} - \epsilon \nabla V(\text{paper})$$ as the following slides show:

Then we're essentially done: assuming the paper was intrinsically white, all darkness in its image must come from low lighting, meaning we just have to scale the brightnesses up: $$\text{drawing} = \text{original} \cdot \frac{255}{\text{paper}}$$ Finally, we clean up a little by rounding all pixels sufficiently bright ($> 248$) to $255$ --- full white. Tada! Although I didn't end up revising the algorithm, I did have a lot of trouble adjusting the stiffness $s$. We want our paper very stiff, that is, at-most-gently curved, so as not to overfit the drawing. Real images of paper seem very stiff. But great stiffness requires a tiny timestep, or we'll overshoot! Indeed, some pretty cool artifacts appear when we use $n = 200$, timesteps of $\epsilon = 0.1$, $m = 10, k = 100$, and varying $s$:

Worry not! Using a finer $n = 1500$, $\epsilon = 0.02$, with stiffer $m, k, s = 10, 100, 30$, our paper is smooth and we get such images as:

That's another copy of a Hokusai sketch, this time Manga 28-3-L. Tada!